Rasha Khaleel1, Lutfi Al-Sharif1, Mazuz Salahat2
1Mechatronics Engineering Department, University of Jordan, Amman 11942, Jordan
2Mechatronics Engineering Department, Faculty of Engineering Technology,
Balqa Applied University, Jordan
This paper was presented at The 3rd Symposium on Lift & Escalator Technology (CIBSE Lifts Group and The University of Northampton) (2013). This web version © Peters Research Ltd 2016
Abstract
The design of vertical transportation systems still heavily relies on the calculation of the round trip time (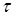 ). The round trip time (
). The round trip time (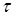 ) is defined as the average time taken by an elevator to complete a full trip around a building. There are currently two methods for calculating the round trip time: the conventional analytical calculation method; and the Monte Carlo simulation method.
) is defined as the average time taken by an elevator to complete a full trip around a building. There are currently two methods for calculating the round trip time: the conventional analytical calculation method; and the Monte Carlo simulation method.
The conventional analytical method is based on calculating the expected number of stops and the expected highest reversal floor and then substituting the values in the main formula for the round trip time. This method makes some assumptions as to the existence of some special conditions (such as equal floor heights and a single entrance). Where these assumptions are not true in a building, this invalidates the use of the analytical formula the use of which will lead to errors in the result. The conventional analytical equation can be further developed to cover some of the special conditions in the building, but they do not cover all of these special conditions and also do not cover combinations of these special conditions.
The simplest round trip time equation makes the following assumptions: equal floor heights, one single entrance, equal floor populations and that the rated speed is attained in one floor jump. The case of unequal floor populations can be accounted for by amending the values of the probable number of stops and the highest reversal by using the formulae for the unequal floor population case.
The work presented in this paper identifies the four special conditions that are assumed in the classical round trip time analytical equation. It then develops analytical formulae for calculating the round trip time equation for any of the four special conditions or any combination of these conditions under incoming traffic conditions.
Keywords: Elevator, lift, round trip time, interval, up peak traffic, basement, entrance, sub-entrance, highest reversal floor, probable number of stops, Monte Carlo Simulation, calculation.
1. Introduction
The planning of vertical transportation systems in any building still depends on evaluation of the round trip time ( 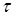 ) during the up peak traffic condition (also referred to as the incoming traffic conditions). The round trip time is the time required by an elevator to complete a full cycle in the building.
) during the up peak traffic condition (also referred to as the incoming traffic conditions). The round trip time is the time required by an elevator to complete a full cycle in the building.
There are currently two methods for calculating the round trip time in the incoming traffic condition (also known as up-peak). The most widely used method is an analytical one and is based on calculating the expected number of stops and the expected highest reversal floor [1], [2]. The other method recently introduced relies on the use of Monte Carlo simulation in order to arrive at the value of the round trip time, without the need to use formulae that are derived from first probability principles [7]. It is important to note that the work in this paper assumes incoming traffic conditions (i.e., up peak traffic conditions).
In order to derive a general formula for calculating the elevator round trip time it is necessary to study the movement of the elevator car around the building in a single trip during up peak traffic conditions. The round trip time comprises the following components:
- The door time: The time required for the elevator doors to open and close during every stop.
- The passenger transfer time: This is the time required by the passengers to board the elevator and alight.
- The up travelling time: This is the time required by the elevator to travel upwards between floors.
- The down travelling time: This is the time required by the elevator to express back from the highest reversal floor back to the main terminal.
Figure 1 shows in a diagrammatic form the movement of the elevator car during a round trip, where the x-axis represents time, the y-axis represents vertical position within the building.
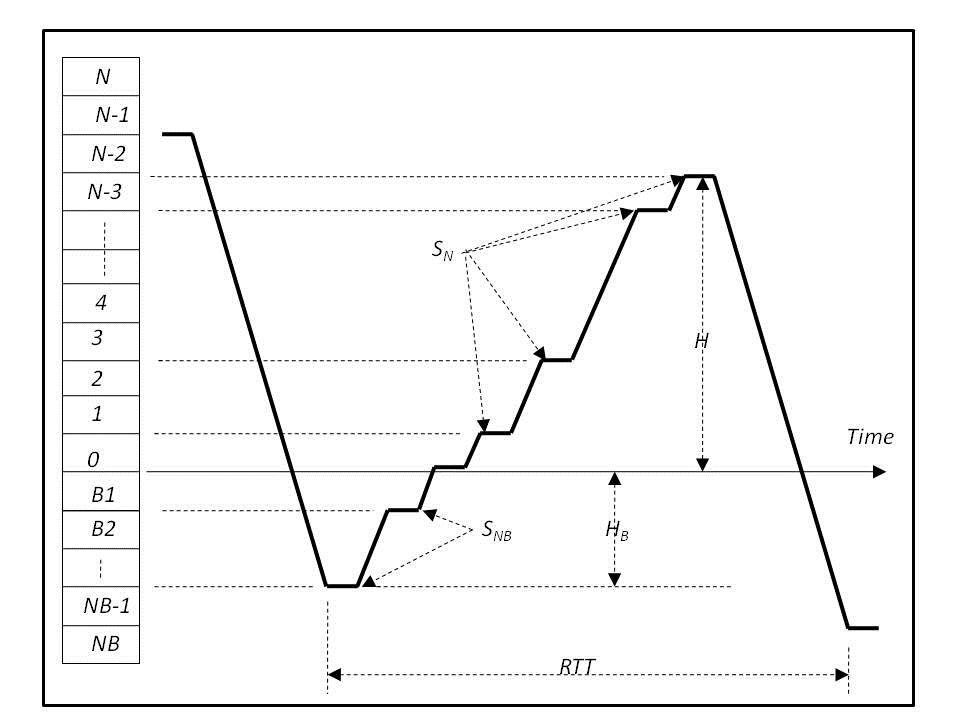
Figure 1: Round trip time timeline where the elevator goes down to the basement.
In describing the types of traffic prevailing in the building, the following three terms will be used:
- Incoming traffic: It describes the traffic entering the building (i.e., all journeys originate at an entrance/exit floor).
- Outgoing traffic: It describes the traffic leaving the building (i.e., all journeys terminate at an entrance/exit floor).
- Inter-floor traffic: This term describes the traffic that circulates within the building (in other words all inter-floor traffic journeys do not originate or terminate at a building entrance floor).
It is convenient to use the classification above in order to describe the prevailing traffic pattern in a building at any point in time. So the prevailing traffic at any one point in time can be described as a mixture of 40% incoming traffic, 40% outgoing traffic and 20% interfloor traffic for example. This is a suitable method of characterizing different traffic patterns at different times of the day in an office building.
Section 2 of this paper reviews the classical analytical method of calculating the round trip time. Section 3 reviews previous work in the area of evaluating the value of the round trip time. Section 4 derives a new equation for the effective floor height when the floor heights are not equal. Section 5 derives the round trip time equation in two stages: the first stage derives it for the case of a single entrance; the second stage adds the condition of multiple entrances. A practical numerical example is given in section 6. Conclusions are drawn in section 7.
2. The Classical Method of calculating of the round trip time
The traditional method used in the design of vertical transportation systems depends on calculation of the round trip time for an elevator during incoming traffic conditions (usually referred to as up peak traffic). Up peak means that all traffic in the building is incoming, and that the elevator collects P of the passengers from the main entrance (usually the ground floor), and then moves in the up direction to deliver them to their destination floors.
The round trip time (τ) is the time taken by the elevator to collect P passengers from the main entrance and get them to their destination floors and return again to the main entrance. The actual value of the round trip time can be determined by finding the expected value of the number of stops (S) that the elevator will make during its service to the passengers and the expected value of the highest reversal floor (H) that the elevator will attain during its journey in the up direction. These two variables (i.e., S and H) are dependent on the number of floors above the main terminal, N, and the number of passengers boarding the elevator from the main terminal, P. The kinematics of the elevator in moving between floors is based on the rated speed, rated acceleration and rated jerk values.
The value of the round trip time ( ) for an elevator during up peak conditions can be calculated as follows [1], [2] and [4]:
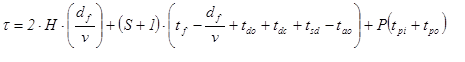 (1)
(1)
where:
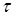 is the round trip time in s
is the round trip time in s
H is the highest reversal floor (where floors are numbered 0, 1, 2….N
S is the probable number of stops (not including the stop at the ground floor)
df is the typical height of one floor in metres
v is the rated speed in metres per second
tf is the time taken to complete a one floor journey in seconds
P is the number of passengers in the car when it leaves the ground floor
tdo is the door opening time in seconds
tdc is the door closing time in seconds
tsd is the motor start delay in seconds
tao is the door advance opening time in seconds (where the door starts opening before the car comes to a complete standstill)
tpi is the passenger boarding time in seconds
tpo is the passenger alighting time in seconds
The probable number of stops S for equal floor populations was first derived in [5]. It can be calculated as follows for equal floor populations:
(2)
The highest reversal floor H was first derived in [6]. It can be calculated as follows for equal floor populations:
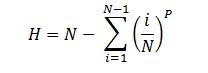
The flight time between floors at any rated speed, acceleration, jerk and travel distance, can be calculated using the formulae in [7], reproduced below:
a. Where the elevator attains rated speed in the journey:
(4)
b. Where the elevator attains rated acceleration in the journey but does not attain rated speed:
(5)
c. Where the elevator attains neither rated acceleration nor speed in the journey:
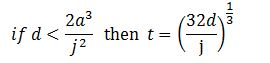
where:
t is the time taken to complete the journey in s
d is the distance of the journey in m
v is the rated speed in m·s-1
a is the rated acceleration in m·s-2
j is the rated jerk in m·s-3
3. Previous Work
Previous work has introduced enhancements to the round trip time calculation methodology in order to deal with special conditions. These are described in the next three sub-sections.
3.1 Unequal Floor Populations
The case of unequal floor populations is dealt with by amending the formulae for calculating the probable number of stops, S, and the highest reversal floor, H. The formulae for the case of unequal floor populations are shown below from [5] and [6] respectively:
(7)
(8)
Where:
Ui is the population of the ith floor
U is the total building population
3.2 Top Speed Not Attained in One Floor Journey
The case where the top speed is not attained in one floor journey has been dealt with in [9]. It is based on the assumption that all floor heights being equal and a single entrance. It derives a formula for the expected number of one floor journeys during a round trip time, two floor journeys, three floor journeys…etc. By multiplying the time taken for each journey length by its probability during a round trip the upward travelling time during the round trip time is calculated.
The formula for a journey of r floors is reproduced below using different notation:
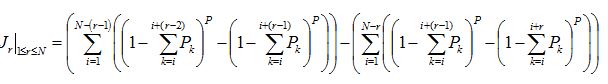
where Pk is the building population expressed as a percentage of the building as calculated below:
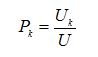
Where:
Jr is the expected number of journeys of length r floors in any round trip
Pk is the percentage of the population on the kth floor
r is the journey length in floors
N is the number of floors above the ground floor
3.3 Multiple Entrances
The case of multiple entrances has been dealt with by calculating the probability of going to the basement and calculating the extra time incurred when the elevator car goes to the basement [3]. The amended formula is shown below, where it is made up of two parts: the original round trip time element for floors above the main entrance and the extra time required to go to the basement multiplied by the probability of going to the basement.
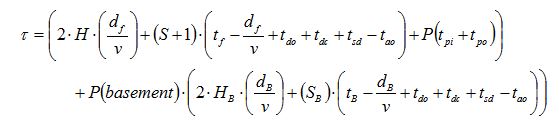
where:
P(basement) is the probability of the elevator going to the floors below ground in any one round trip.
dB is the floor height of the basement floors in m
tB is the time to traverse one basement floor in s
SB is the expected number of stops in the basement
HB is the expected highest reversal floor in the basement
This paper first addresses the fourth special condition: the case of unequal floor heights. This is done in the next section. It then develops a universal formula for the round trip time that can deal with all four conditions combined. This is done in section 5.
4. Unequal Floor Heights Formula Derivation
In the case where the floor heights are unequal, this will have an effect on the calculation of the round trip time equation. The equation for the round trip time can be amended in order to account for this case as follows.
The effect of the unequal floor heights can be taken into consideration by assuming an effective floor height df eff that can be inserted into the original round trip time equation in place of df.
The effective floor height df eff is the expected value of the floor height. The effective floor height is the weighted average of the product of each floor height multiplied by the probability of the elevator passing through that floor. In order for the elevator to pass through a floor it should travel to any of the floors above that floor. Thus it is necessary to find the probability of the elevator travelling above a certain floor, i.
The probability of the elevator not stopping at a certain floor, assuming equal floor populations is the probability that passenger j will stop at a floor i:
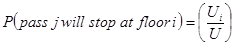 (12)
(12)
where N is the number of floors above the ground floor. Thus the probability that passenger j will not stop at a floor i is:
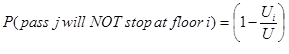 (13)
(13)
But the car contains P passengers. So the probability that none of them will stop at floor i is the product of all of their respective probabilities:
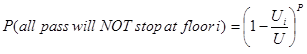 (14)
(14)
The probability that the lift will not travel any higher than a floor i is the probability that it will not stop on floor i+1 or i+2 or i+3 all the way to floor N. This is expressed as the product of these individual probabilities:
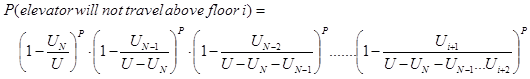 (15)
(15)
This can be re-written as:
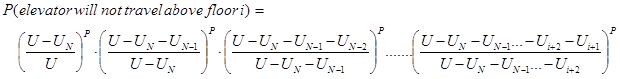 (16)
(16)
Putting all terms inside the same bracket gives:
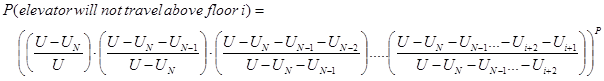 (17)
(17)
This simplifies to:
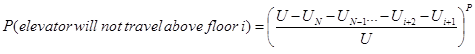 (18)
(18)
This can be further simplified to the following expression:
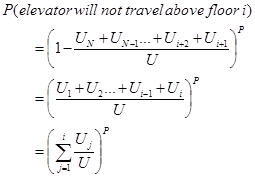 (19)
(19)
The probability that the lift will travel above floor i is:
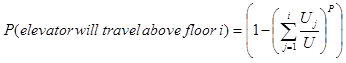 (20)
(20)
There are two special cases worth considering. The first is the case where i=N. Substituting a value of N for i results in the probability of the elevator traversing that floor is zero (this is obvious as the elevator cannot travel above the Nth floor). The second case is the case where i=0, where the probability is one. This is also obvious as the elevator will definitely go through the height of the ground floor.
Thus the expected value of the travel distance can be calculated as the weighted average of the various floor heights as follows:
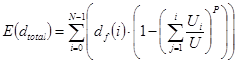 (21)
(21)
Where:
E(dtotal) is the expected value of the distance travelled in the up direction in m.
This variable is a distance and thus it has units of m (rather than floors).
It is worth noting that the summation runs from 0 to N-1 (i.e., rather than 1 to N). This is in recognition of the fact that the height of the floor N is irrelevant as the elevator will never traverse that floor height. The 0 index denotes the fact that the elevator will always traverse the ground floor height.
The expected floor height is obtained by dividing the expected total travel distance by the highest reversal floor, H. So the equation for the effective floor height can be expressed as shown below:
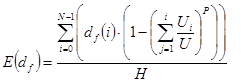 (22)
(22)
Substituting the expression for the highest reversal floor based on the general case of unequal floor population, provides the final expression for the effective floor height unequal floor heights:
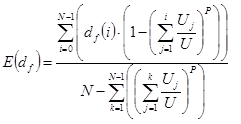 (23)
(23)
Where:
df(i) is the floor height for floor i in m
E(df) is the expected value of the floor heights (effective floor height) which has units of m/floor
H is the highest reversal floor
N is the number of floors above the main terminal
P is the number of passengers boarding the car from the main terminal
It is important to note that formula (23) is only applicable under incoming traffic conditions.
Having derived the formula for the effective floor height under unequal floor heights as well as unequal floor populations provides a tool to address the issue of unequal floor heights, provided that the top speed is attained in one floor journey. The resulting value from formula (23) can be substituted as the effective floor height in the general round trip time formula shown in (1) in place of df.
5. Derivation of the Round Trip Equation for the General Case
The last section tackled the special case of the unequal floor heights combined with unequal floor populations. It allowed the calculation of the round trip time where the floor heights are unequal and the floor populations are unequal for a building with a single entrance. However, it cannot be used in the case where the top speed is not attained in one floor journey.
In this section, the round trip time formula is derived for the case where the top speed is not attained in one floor journey, where the floor heights are unequal and where the floor populations are unequal for a building with multiple entrances.
The first subsection derives the formula for the round trip time under the first three special conditions (top speed not attained, unequal floor heights and unequal floor populations). The second subsection amends the formula to cover the case for multiple entrances.
5.1 Floor round trip time equation derivation assuming a single entrance
In order to develop the universal round trip equation, it is necessary to subdivide the round trip time in a way different to that previously followed. For the purposes of this derivation, there are a number of time components that make up the total round trip time as follows:
- Passenger boarding and alighting time. This will be denoted as tP.
- Door closing and opening times. This is repeated a number of times equal to the number of stops plus one stop (for the main entrance). This will be denoted as tD.
- Time to travel in the upward direction to deliver the P passengers to the upper floors. This will be denoted as tU.
- Time to travel back from the highest reversal floor back down the main entrance. This will be denoted as tH.
These components are summarized in equation (24) below.
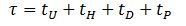
Components a) and b) are stationary time components, while components c) and d) are travelling time components. A full expression for the round trip will be derived below, based on a single entrance.
An office building with N floors above ground is assumed, where the ground floor is the only entrance to the building. The elevator car fills up with P passengers on average as it leaves the ground floor. Each of the floors has a population denoted as Uk, where Uk is the population of floor k. Based on the definition above, it is clear that sum of all the populations divided by the total building population is equal to 1 as shown in (25) below.
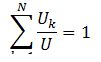
The probability of a journey of r floors starting from the ground floor in the upward direction is [9]:
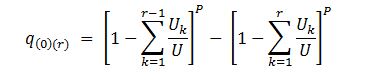
Moreover, the probability of a journey of r floors from floor i to floor j can be calculated as shown below (where j=i+r):
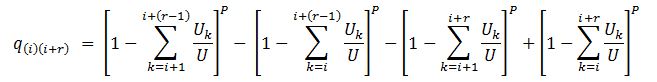
For each value of r, there are a number of journeys of length r floors. Each possible journey of r floors contributes to the round trip time. Each journey requires a time element that is equal to the time required to travel between the two floors, i and j. The contribution of such an element is equal to the product of the probability of the journey taking place and the time this actually takes.
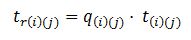
For each value of r, there are two parts: one journey from the ground floor up r floors and then all other possible journeys of length r starting from upper floors. So the contribution to the round trip time from each value of r is the summation of all possible terms:
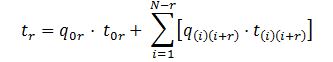
Where t(i)(i+r) is time required to travel between floors i and i+r. This can be calculated based on the distance, rated speed, rated acceleration and rated jerk, using the formulae found in [8]. It is worth noting that r can vary from the value of 1 (i.e., one floor journey) up the value of N (i.e., one journey running from the ground floor to the topmost floor covering N floors). So the total time spent by the elevator travelling in the up direction is the sum of the term in equation (29) over all possible values of r (1 to N).
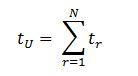
The next step is to calculate the time component tH. This is the time required by the elevator to express back from the highest reversal floor back to the ground floor. As the floor heights are not equal, it is not possible to merely multiply the value of the highest reversal floor (H) by the floor height.
The total distance that has to be travelled can be found from equation (21), reproduced below.
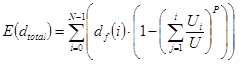 (31)
(31)
Using the kinematic equations ((4), (5) and (6)), the time taken to traverse this distance can be found and is equal to tH.
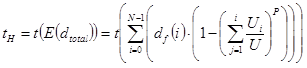 (32)
(32)
where the function t(d) is the time in s taken to traverse a distance d based on rated speed, rated acceleration and rated jerk.
The third term, tD, in equation (24) represents the door time. The doors will open and close a number of times equal to the expected number of stops plus one (one extra stop is required at the ground floor to load passengers). The calculation of the term requires the calculation of the number of stops, S and the values of the door opening time, door closing time, motor start delay and the advanced door opening time.
In order to calculate the expected number of stops, the equation below shall be used (which is based on the general assumption of unequal floor populations). It is worth noting that the calculation of S is not affected by the case of unequal floor heights or the case of top speed not attained in one floor journey.
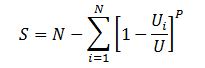
The door time, tD can thus be calculated using the formula (34) below:
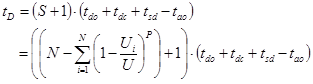 (34)
(34)
The fourth and final term in the round trip time equation represents the passenger boarding and alighting time and is denoted by tP. It is easy to calculate by multiplying the number of passengers by the sum of the boarding and alighting time per passenger, as shown below:
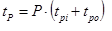 (35)
(35)
Combining all four equations into the round trip time equation, gives the full equation for the round trip under the three special conditions (unequal floor heights, unequal floor populations and top speed not attained):
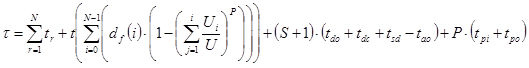 (36)
(36)
5.2 Expansion of the Formula for multiple entrances
In order to account for the effect of multiple entrances, equation (36) is amended in order to allow for the presence of basements, using an approach similar to that in [3].
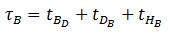
where:
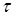 B is the average extra time added to the round trip time of the elevator when the elevator goes to the basement
B is the average extra time added to the round trip time of the elevator when the elevator goes to the basement
tBD is the time to travel in the upward direction in the basements to collect the P passengers.
tDB is the door closing and opening times in the basement floors . This is repeated a number of times equal to the number of stops in the basements floors.
tHB is the time to travel down to the basement’s highest reversal floor.
Expanding (37) gives:
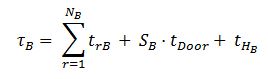
where:
trB is time taken to traverse a journey of r floors
NB is the number of basement floors
SB is expected number of stops in the basement
tDoor is the time taken by the doors to complete a full opening/closing cycle
Expanding (38) gives:
The general equation for calculating the universal round trip time in the general case assuming up peak traffic conditions and the presence of basements is shown below:
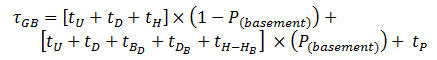
P(basement) is the probability that the elevator will go to at least one of the basements (sub-entrances) in a round trip journey (which is equal to the probability of the elevator going to the basement in any one round trip journey). The formula for calculating this probability is shown below:
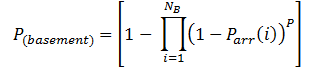
6. Practical Example
In order to illustrate the application of the equation, a practical example is given and solved below.
An office building has a total of 18 floors: 14 office floors above ground, one ground floor and three car-park basement floors under the ground floor. The floor populations, arrival rates and floor heights are shown in the table below:
Table 1: Floor heights, population and arrival rates in the building.
| Floor | Floor height (m) | Floor population | Arrival percentage (%) |
| L14 | 4 | 50 | - |
| L13 | 4 | 50 | - |
| L12 | 4 | 100 | - |
| L11 | 4 | 100 | - |
| L10 | 4.5 | 100 | - |
| L9 | 4.5 | 100 | - |
| L8 | 4.5 | 100 | - |
| L7 | 4.5 | 100 | - |
| L6 | 4.5 | 100 | - |
| L5 | 4.5 | 100 | - |
| L4 | 4.5 | 100 | - |
| L3 | 4.5 | 100 | - |
| L2 | 4.5 | 150 | - |
| L1 | 4.5 | 150 | - |
| G | 5.0 | - | 85% |
| B1 | 3.2 | - | 5% |
| B2 | 3.2 | - | 5% |
| B3 | 3.2 | - | 5% |
The following parameters will be assumed:
Table 2: Traffic analysis parameters.
| Parameter | Value |
| Arrival rate | 12% |
| Target interval | 30 s |
| Passengers | 16.8 |
| Door opening time | 2 s |
| Door closing time | 3 s |
| Motor start delay | 0.5 s |
| Advanced door opening | 0 s |
| Rated speed | 4.0 m·s-1 |
| Rated acceleration | 1.0 m·s-2 |
| Rated jerk | 1.0 m·s-3 |
| Passenger boarding time | 1.2 s |
| Passenger alighting time | 1.2 s |
The first step is to calculate the round trip time without the presence of basements. The equation for the round trip time where the only entrance is the ground floor (G) can be written as follows:
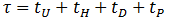
Where:
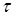 is the round trip time in s
is the round trip time in s
tU is the time to travel in the upward direction to deliver the P passengers to the upper floors.
tH is the time to travel back from the highest reversal floor back down to the main entrance.
tD is the door closing and opening times. This is repeated a number of times equal to the number of stops plus one stop (for the main entrance).
tP is the passenger boarding and alighting time.
The time to deliver P passengers in the upward direction to the upper floors can be calculated from equations (29) and (30). This gives the following value:
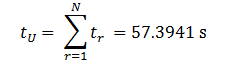
The expected running time in the down direction tH can be found by using the expected value of the total floor heights E(dtotal) as shown in equation (21):
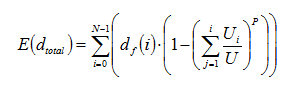
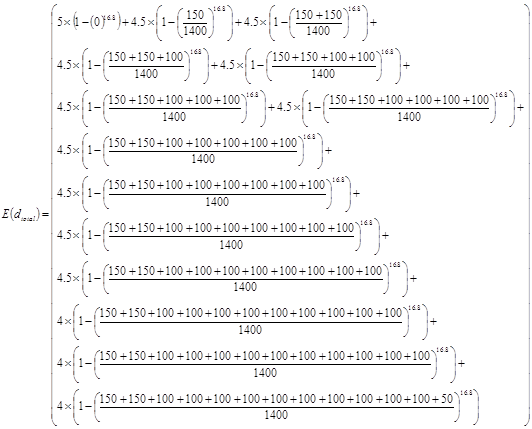 (45)
(45)
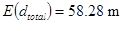 (46)
(46)
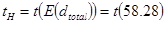 (47)
(47)
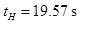 (48)
(48)
Using the value of P of 16.8 passengers, the probable number of stops S can be calculated as follows (assuming unequal floor population) using equation (7):
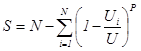 (49)
(49)
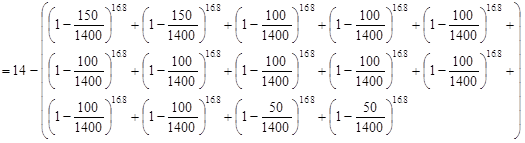 (50)
(50)
S = 9.737
The door time, tD can also be calculated as follows:
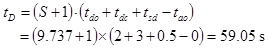 (51)
(51)
The passenger boarding and alighting time, it is easy to calculate, as shown below:
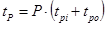 (52)
(52)
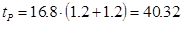 (53)
(53)
Substituting in the round trip time equation (24) gives:
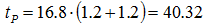 (54)
(54)
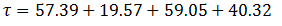
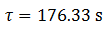 (56)
(56)
Using Monte Carlo simulation (at 10 000 runs) gives a value of the round trip time of 176.377 s. Applying the formulae developed in this paper gives a value for the round trip time of 176.33 s.
The value of the round trip time where the elevator serves the ground and the basements is given as follows:
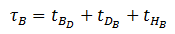
Where:
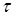 B is the average additional time added to the round trip time of the elevator where the elevator goes to the basement in every journey
B is the average additional time added to the round trip time of the elevator where the elevator goes to the basement in every journey
tBD is the time to travel in the upward direction in the basements to collect the P passengers.
tDB is the door closing and opening times in the basements floors . This is repeated a number of times equal to the number of stops in the basements floors.
tHB is the time to travel down to the basement highest reversal floor.
The time to collect P passengers from basements floors in the upward direction to the main entrance can be calculated from equations (29) and (30).
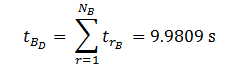
Using the value of PB passengers originating in the basements, the number of stops in the basements SB can calculated as follows (assuming unequal floor population), which is a reformulation of equation (7) for arrival floors:
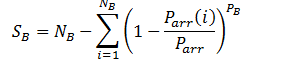
Where
SB is the expected number of stops in the basement
NB is the number of basement floors
PB is the number of passengers arriving in the basements
Parr(i) is the percentage arrival from the ith arrival floor
The critical parameter that decides the value of SB is PB which is the number of passengers that are picked up from the basements. This is decided by the total percentage arrivals from the basement and can be evaluated as follows:
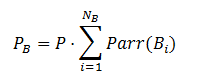
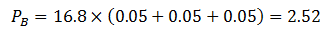
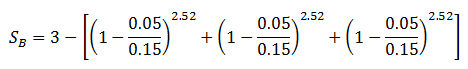
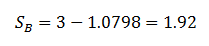
The door time, tDB can be calculated as follows:
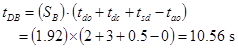 (64)
(64)
The expected running time in the down direction tHB in the basement floor can be found by using the expected value of the total basement heights E(dB(total)) using a modified version of equation (44) for the basements and applying the results from the kinematic equations (4), (5) and (6) as follows:
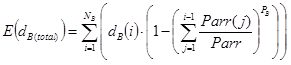 (65)
(65)
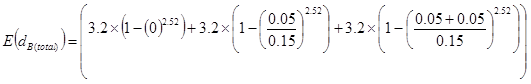 (66)
(66)
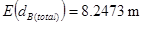 (67)
(67)
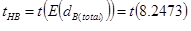 (68)
(68)
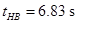 (69)
(69)
The average extra time added to the round trip time of the elevator when the elevator goes to the basement in every journey is:
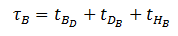
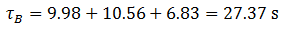
The universal round trip time is:
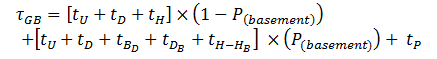
Where tH-HB is the flight time for the elevator to travel from the effective highest reversal floor (H) to the effective highest reversal basement floor (HB) in the down direction, which equals the time needed to pass through distance E(dB(total)) (total effective basement height) and E(dtotal) (total effective floor height), evaluated using the kinematic equations (4), (5) and (6).
It is evaluated as follows:
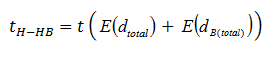
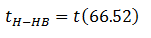
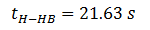
The probability that the elevator will go to at least one of the basements (sub-entrances) in a round trip journey is calculated as follows:
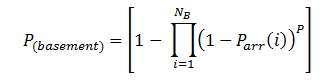
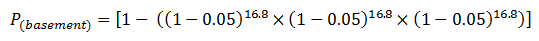
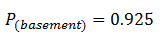
The universal round trip time can thus be calculated using equation (72) as follows:

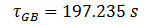
Using Monte Carlo simulation (at 1000 runs) gives a value of the round trip time of 197.165 s. Applying the formulae developed in this paper gives a value for the round trip time of 197.235 s.
It is worth noting that all the four special conditions apply in the case of this building: Top speed not attained in one floor journey, unequal floor heights, unequal floor population and multiple entrances.
7. Conclusions
The widely used equation or the round trip time assumes a number of special conditions, namely: equal floor heights, equal floor populations, top speed attained in one floor journey and single entrance.
In this paper a new formula has been derived in order to address the problem of unequal floor heights. Moreover, a set of equations has been derived in order to deal with all four special conditions combined. A numerical example has been fully worked out in order to find the value of the round trip time. The result was successfully verified using the Monte Carlo simulation method.
REFERENCES
- G. C. Barney, “Elevator Traffic Handbook: Theory and Practice”, Spon Press, London and New York, ISBN 0-415-27476-1, 438 p., 2003.
- CIBSE, CIBSE Guide D, “Transportation Systems in Buildings”, Third edition, The Chartered Institute of Building Services Engineers, 2005.
- Lutfi Al-Sharif, “The effect of multiple entrances on the elevator round trip time under up-peak traffic”, Mathematical and Computer Modelling 52(3-4):545-555 (2010).
- G. R. Strakosch, “Vertical transportation handbook, 3rd edition“, Wiley, (1998).
- Basset Jones, “The probable number of stops made by an elevator“, General Electric Review 26 (8), 1923.
- J. Schroeder, “Personenaufzuege, Foerden und Heben”, 1955.
- Lutfi Al-Sharif, Hussam Dahyat, Laith Al-Kurdi, “ The use of Monte Carlo Simulation in the calculation of the elevator round trip time under up-peak conditions”, Building Services Engineering Research and Technology, volume 33, issue 3 (2012) pp. 319–338, doi:10.1177/0143624411414837.
- R. D. Peters, “Ideal lift kinematics: derivation of formulae for the equations of motion of a lift“, International Journal of Elevator Engineers, 1996.
- N.R. Roschier, M.J. Kaakinen, “New formulae for elevator round trip time calculations”, Elevator World supplement, 1978.
- R. D. Peters, “Vertical transportation planning in building EngD thesis“, Uxbridge: Brunel University, 1997.
BIOGRAPHICAL DETAILS
Lutfi Al-Sharif received his Ph.D. in lift traffic analysis in 1992 from the University of Manchester. He worked for 9 years for London Underground, London, United Kingdom in the area of lifts and escalators. In 2002, he formed Al-Sharif VTC Ltd, a vertical transportation consultancy based in London, United Kingdom. He has 17 published papers in peer reviewed journals the area of vertical transportation systems and is co-inventor of four patents. He is currently Associate Professor in the Department of Mechatronic Engineering at The University of Jordan, Amman, Jordan.
